
Cos (a + b) Formula, Proof, Examples What is Cos(a + b)?
Formula ( 1). cos ( a − b) = cos a cos b + sin a sin b ( 2). cos ( x − y) = cos x cos y + sin x sin y Introduction Let a and b be two variables, which are used to represent two angles in this case. The subtraction of angle b from angle a is the difference between them, and it is written as a − b, which is a compound angle.

Trigonometric Addition and Difference Formulas (Identities) Also double angle formulas. hubpages
The formula of cos (A + B) is cos A cos B - sin A sin B. Example : If sin A = 3 5 and cos B = 9 41, find the value of cos (A + B). Solution : We have, sin A = 3 5 and cos B = 9 41 ∴ cos A = 1 - s i n 2 A and sin B = 1 - c o s 2 B cos A = 1 - 9 25 = 4 5 and sin B = 1 - 81 1681 = 40 41 Now, By using above formula,

law of cosines Law of cosine (cosine law)
Formula ( 1). cos ( a + b) = cos a cos b − sin a sin b ( 2). cos ( x + y) = cos x cos y − sin x sin y Introduction Let us consider that a and b are two variables, which denote two angles. The sum of two angles is written as a + b, which is actually a compound angle.
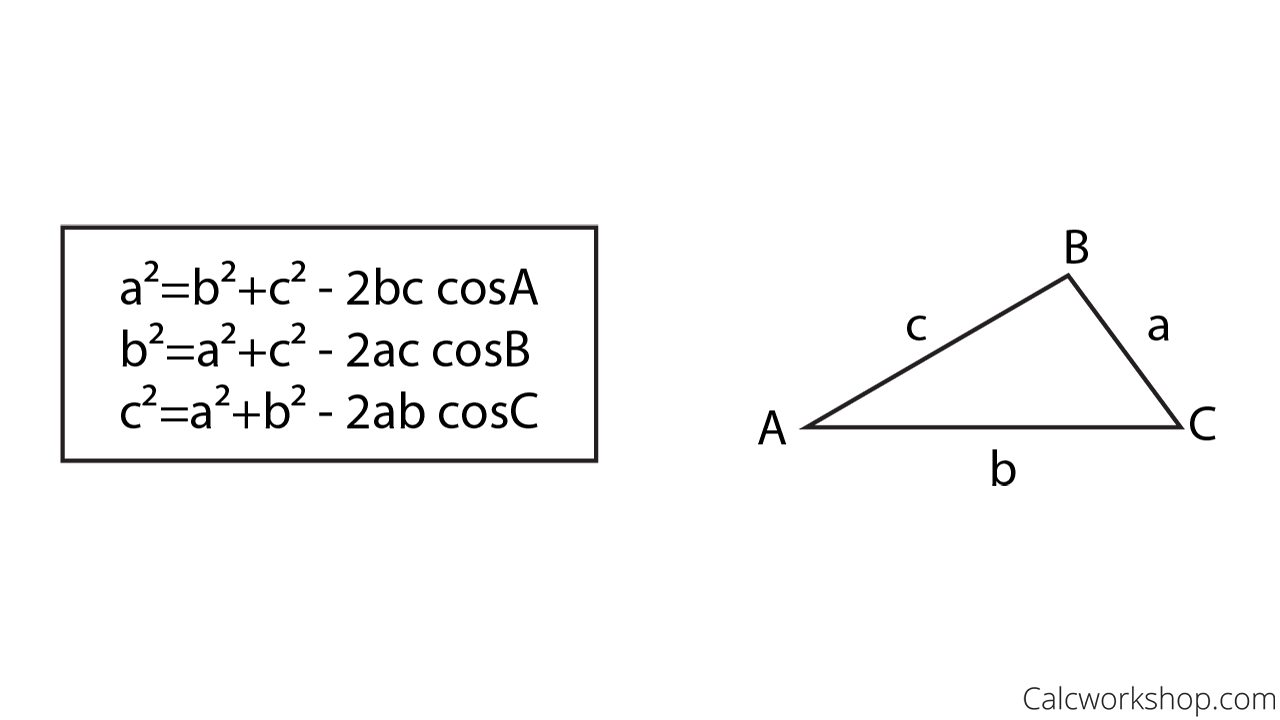
What is the Law of Cosines? (Explained in 3 Powerful Examples!)
Get Started Cos (a + b) In trigonometry, cos (a + b) is one of the important trigonometric identities involving compound angle. It is one of the trigonometry formulas and is used to find the value of the cosine trigonometric function for the sum of angles. cos (a + b) is equal to cos a cos b - sin a sin b.

Cos (a b) Formula, Proof, Examples What is Cos(a b)?
Learn to derive the formula of cos (A + B). Proof of expansion of cos(A+B). cos (A +B) is an important trigonometric identity. We all learn the expansion and.
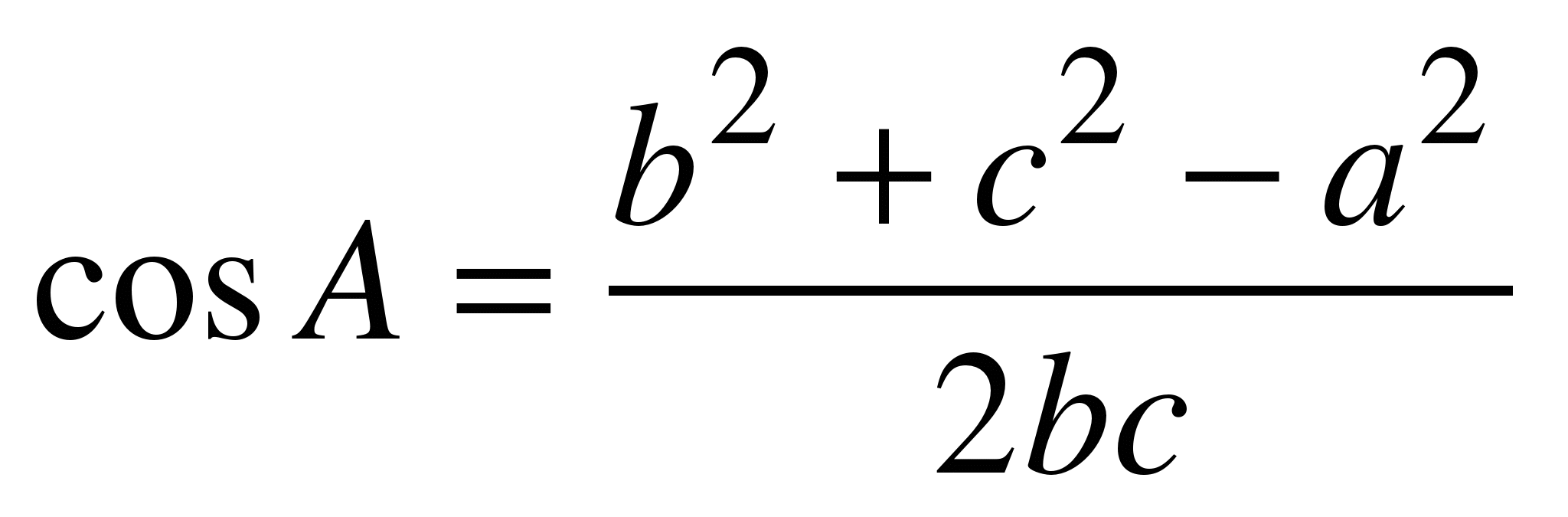
the Cosine Rule National 5 Maths
cos^2(a + b) = cos^2(a) + cos^2(b) - 2cos(a)cos(b). Proof of Cos(a + b) Formula. The cos(a+b) formula is a mathematical expression used to determine the angle of two vectors. The formula is derived from the law of cosines, which states that the cosine of the angle between two vectors is equal to the product of their magnitudes and the sum of.
The Cosine Rule IGCSE at Mathematics Realm
Cosines Tangents Cotangents Pythagorean theorem Calculus Trigonometric substitution Integrals ( inverse functions) Derivatives v t e In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined.

Cos A Cos B Cos C Communauté MCMS
In trigonometry, cos (a - b) is one of the important trigonometric identities, that finds application in finding the value of the cosine trigonometric function for the difference of angles. The expansion of cos (a - b) helps in representing the cos of a compound angle in terms of trigonometric functions sine and cosine.

Trigonometry
Because of all that we can say: sin (θ) = 1/csc (θ) cos (θ) = 1/sec (θ) tan (θ) = 1/cot (θ) And the other way around: csc (θ) = 1/sin (θ) sec (θ) = 1/cos (θ) cot (θ) = 1/tan (θ) And we also have: cot (θ) = cos (θ)/sin (θ) Pythagoras Theorem

IDENTIDADES TRIGONOMÉTRICAS PARA LA SUMA Y RESTA DE ÁNGULOS
Cos a Cos b is a trigonometric formula that is used in trigonometry. Cos a cos b formula is given by, cos a cos b = (1/2) [cos (a + b) + cos (a - b)].

Law of Cosine (Cosine Law) with Examples and Proof Teachoo
Product to Sum Formulas sin x sin y = 1/2 [cos (x-y) − cos (x+y)] cos x cos y = 1/2 [cos (x-y) + cos (x+y)] sin x cos y = 1/2[sin(x+y) + sin(x−y)] cos x sin y = 1/2[sin(x+y) - sin(x−y)] Sum to Product Formulas sin x + sin y = 2 sin [ (x+y)/2] cos [ (x-y)/2] sin x - sin y = 2 cos [ (x+y)/2] sin [ (x-y)/2]

cos(A+B) YouTube
Trigonometric Identities are useful whenever trigonometric functions are involved in an expression or an equation. Trigonometric Identities are true for every value of variables occurring on both sides of an equation. Geometrically, these identities involve certain trigonometric functions (such as sine, cosine, tangent) of one or more angles.. Sine, cosine and tangent are the primary.

Cos A B Formula TRANSFORMACIONES TRIGONOMÉTRICAS DE SUMA A PRODUCTO Y DE Formulas for
The Law of Cosines (also called the Cosine Rule) says: c 2 = a 2 + b 2 − 2ab cos (C) It helps us solve some triangles. Let's see how to use it. Example: How long is side "c". ? We know angle C = 37º, and sides a = 8 and b = 11 The Law of Cosines says: c2 = a2 + b2 − 2ab cos (C) Put in the values we know: c2 = 82 + 112 − 2 × 8 × 11 × cos (37º)

Trigonometry
Trigonometric Identities Purplemath What is an identity? In mathematics, an "identity" is an equation which is always true, regardless of the specific value of a given variable. An identity can be "trivially" true, such as the equation x = x or an identity can be usefully true, such as the Pythagorean Theorem's a2 + b2 = c2 MathHelp.com

Useful trigonometric identities
The formula of cos (a+b)cos (a-b) is given by cos (a+b)cos (a-b) = cos 2 a -sin 2 b. In this post, we will establish the formula of cos (a+b) cos (a-b). Note that cos (a+b) cos (a-b) is a product of two cosine functions. We will use the following two formulas: cos (a+b) = cos a cos b - sin a sin b. (i) cos (a-b) = cos a cos b + sin a sin b. (ii)

Understanding Cos A+B Formula
The trigonometric identity Cos A - Cos B is used to represent the difference of cosine of angles A and B, Cos A - Cos B in the product form using the compound angles (A + B) and (A - B). We will study the Cos A - Cos B formula in detail in the following sections. Cos A - Cos B Difference to Product Formula