
How To Calculate Sin Haiper
When we divide Sine by Cosine we get: sin (θ) cos (θ) = Opposite/Hypotenuse Adjacent/Hypotenuse = Opposite Adjacent = tan (θ) So we can say: tan (θ) = sin (θ) cos (θ) That is our first Trigonometric Identity. Cosecant, Secant and Cotangent We can also divide "the other way around" (such as Adjacent/Opposite instead of Opposite/Adjacent ):

What are sin cos tan? Chapter 8 Class 10 Trignometric Ratios
GCSE Trigonometry - Intermediate & Higher tier - WJEC Sin, cos and tan Trigonometric relationships are very important in the construction and planning industry and allow precise calculation of.

What Comes After Trigonometry? 17 Most Correct Answers
Three trigonometric ratios Trigonometry involves three ratios - sine, cosine and tangent which are abbreviated to \ (\sin\), \ (\cos\) and \ (\tan\). The three ratios are calculated by.

Contoh Soal Matematika Sin Cos Tan Berbagi Contoh Soal Riset
Sines Cosines Tangents Cotangents Pythagorean theorem Calculus Trigonometric substitution Integrals ( inverse functions) Derivatives v t e Basis of trigonometry: if two right triangles have equal acute angles, they are similar, so their corresponding side lengths are proportional.

Example 11 Show sin1 12/13 + cos1 4/5 + tan1 63/16 = pi
cis is a mathematical notation defined by cis x = cos x + i sin x, [nb 1] where cos is the cosine function, i is the imaginary unit and sin is the sine function. x is the argument of the complex number (angle between line to point and x-axis in polar form ).

How to get sin & cos in an easy way (Hand) YouTube
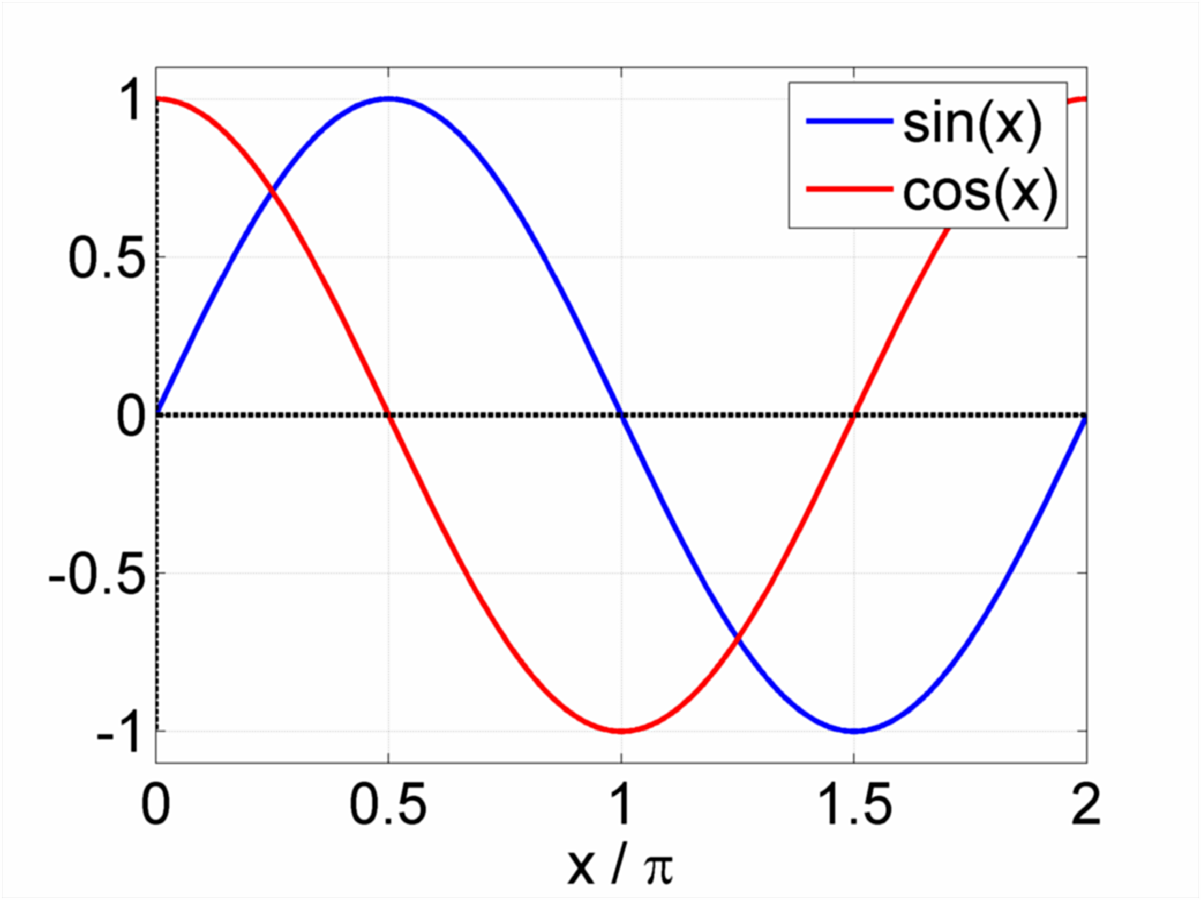
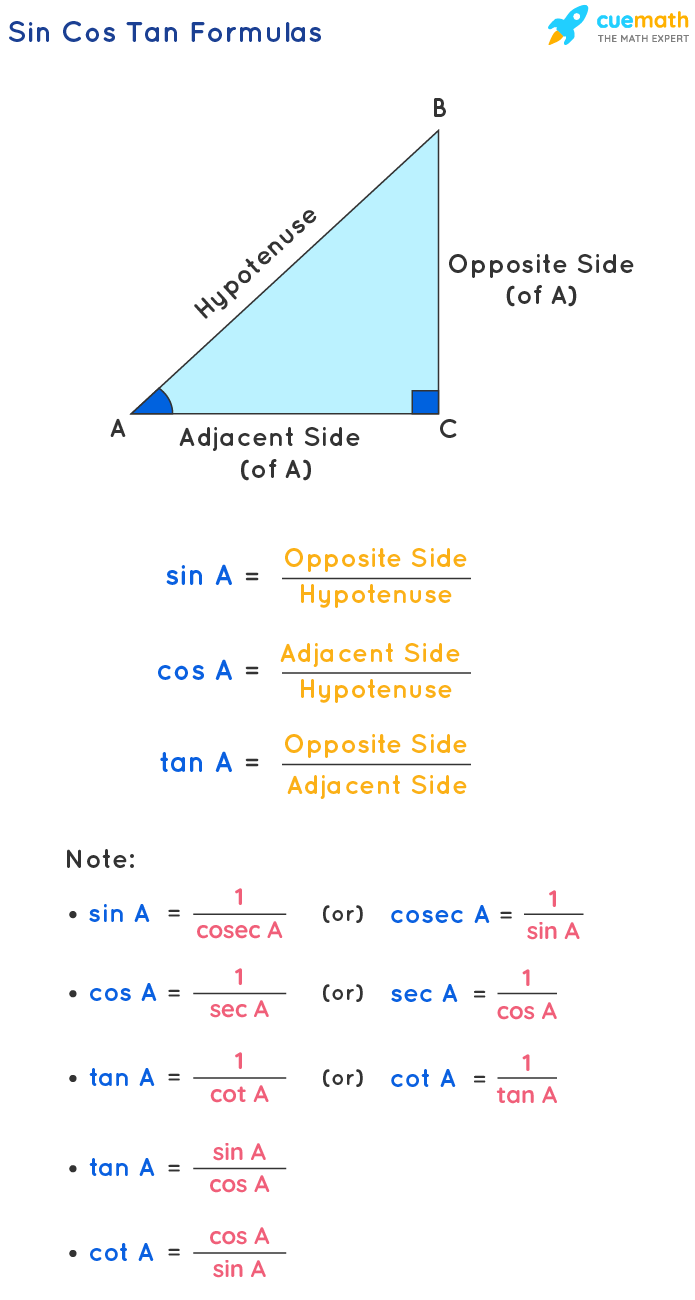
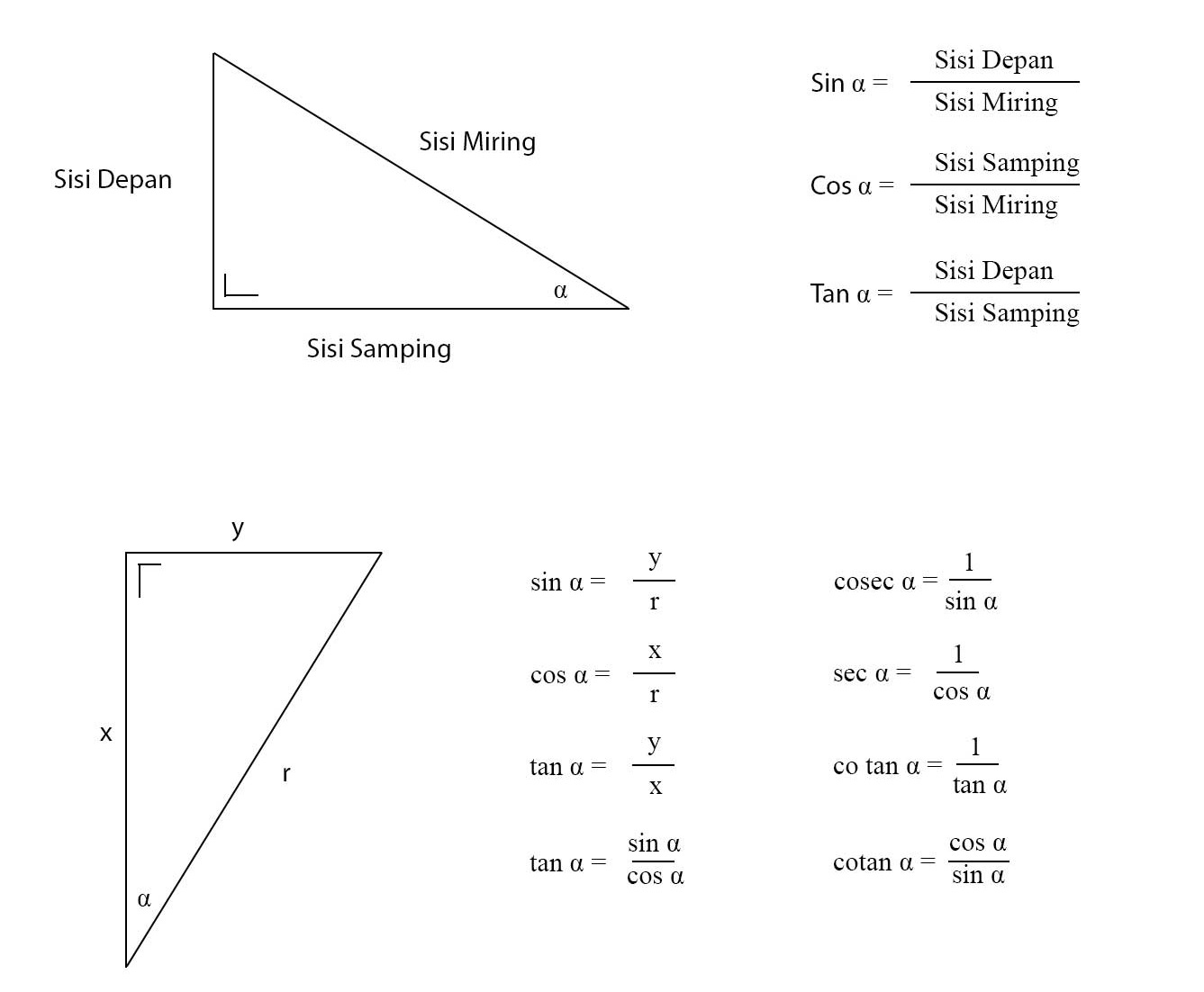
Sine, Cosine and Tangent are the main functions used in Trigonometry and are based on a Right-Angled Triangle. Before getting stuck into the functions, it helps to give a name to each side of a right triangle: "Opposite" is opposite to the angle θ "Adjacent" is adjacent to (next to) the angle θ "Hypotenuse" is the long one
Trigonometric Pythagorean Identity, extended Florians Blog Simple
De nition (Cosine and sine). Given a point on the unit circle, at a counter-clockwise angle from the positive x-axis, cos is the x-coordinate of the point. sin is the y-coordinate of the point. The picture of the unit circle and these coordinates looks like this:

sin cos tan formulas
Purplemath What is an identity? In mathematics, an "identity" is an equation which is always true, regardless of the specific value of a given variable. An identity can be "trivially" true, such as the equation x = x or an identity can be usefully true, such as the Pythagorean Theorem's a2 + b2 = c2 MathHelp.com Need a custom math course?

Misc 4 Prove (cos x cos y)2 + (sin x sin y)2 Chapter 3
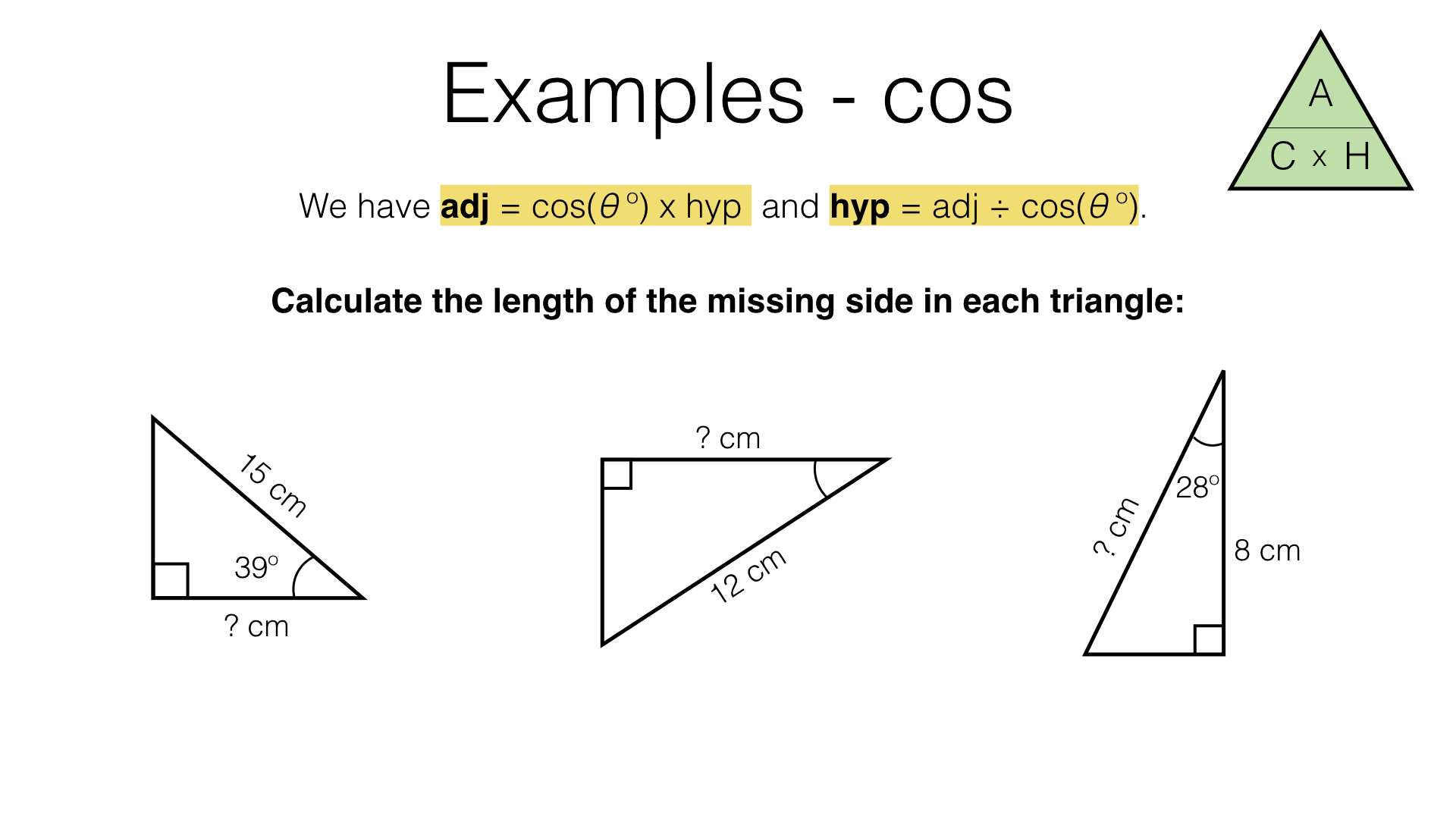
Want to learn more about the law of cosines? Check out this video. Practice set 1: Solving triangles using the law of sines This law is useful for finding a missing angle when given an angle and two sides, or for finding a missing side when given two angles and one side. Example 1: Finding a missing side Let's find A C in the following triangle:
Sin Cos Tan Triangle Calculator Cheapest Wholesalers, Save 52 jlcatj
Trigonometry involves three ratios - sine, cosine and tangent which are abbreviated to \(\sin\), \(\cos\) and \(\tan\). The three ratios can be found by calculating the ratio of two sides of a.

Fitfab Sin Cos Periodic Table
4 Answers Sorted by: 3 In Complex Analysis, we define sin z = z − z3 3! + z5 5! − ⋯ and cos z = 1 − z2 2! + z4 4! − ⋯ sin z = z − z 3 3! + z 5 5! − ⋯ and cos z = 1 − z 2 2! + z 4 4! − ⋯ In particular sin i = i − i3 3! + i5 5! − ⋯ = i ×(1 + 1 3! + 1 5! + ⋯) = sinh(1)i. sin i = i − i 3 3! + i 5 5! − ⋯ = i × ( 1 + 1 3! + 1 5! + ⋯) = sinh ( 1) i.
MATH ONLINE sin cos 2
The basic relationship between the sine and cosine is given by the Pythagorean identity: where means and means This can be viewed as a version of the Pythagorean theorem, and follows from the equation for the unit circle.

What are sin cos tan? SOHCAHTOA With Examples Teachoo
Free math problem solver answers your trigonometry homework questions with step-by-step explanations.
Trigonometry Sin Cos Tan Solver
The three basic trigonometric functions are: Sine (sin), Cosine (cos), and Tangent (tan). What is trigonometry used for? Trigonometry is used in a variety of fields and applications, including geometry, calculus, engineering, and physics, to solve problems involving angles, distances, and ratios. Show more Why users love our Trigonometry Calculator
Belajar Sin Cos Tan Rumus Dengan Mudah Panduan Lengkap Untuk Pemula
where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted cis x ("cosine plus i sine"). The formula is still valid if x is a complex number, and is also called Euler's formula in this more general case.

sin cos tan uitleg overstaand en aanliggend YouTube
cos x - cos y = -2 sin( (x - y)/2 ) sin( (x + y)/2 ) Trig Table of Common Angles; angle 0 30 45 60 90; sin ^2 (a) 0/4 : 1/4 : 2/4 : 3/4 : 4/4 : cos ^2 (a) 4/4 : 3/4 : 2/4 : 1/4 : 0/4 : tan ^2 (a) 0/4 : 1/3 : 2/2 : 3/1 : 4/0 ; Given Triangle abc, with angles A,B,C; a is opposite to A, b opposite B, c opposite C: